Solution Could Someone Help Me Graph Y X 2 4
Of course, (b) is the complete factorization, (a) is not Comparing the results in (a) and (b), we can get x 4 x 2 y 2 y 4 = (x 2 xy y 2)(x 2 –xy y 2)(y^2) = 4(x^2) => y = sqrt 4(x^2) or y = sqrt 4(x^2) Where x belongs to 2,2 Now if we represent it on graph the function will look as shown below
X^2+y^2/4=1
X^2+y^2/4=1-Click here👆to get an answer to your question ️ Factorise x^4 x^2y^2 y^4 Solve Study Textbooks Guides Join / Login Question Factorise x 4 x 2 y 2 y 4 ADivide y, the coefficient of the x term, by 2 to get \frac {y} {2} Then add the square of \frac {y} {2} to both sides of the equation This step makes the left hand side of the equation a perfect square x^ {2}yx\frac {y^ {2}} {4}=4y^ {2}\frac {y^ {2}} {4} Square \frac {y} {2}

Convert X 2 Y 2 4 Into A Polar Equation
$$\begin{align} x^2 y^2 &= r^2\sin^2(\theta)\\ z^2 &= r^2 \cos(\theta) \\ x^2 y^2 z^2&=r^2(\sin^2(\theta) \ Stack Exchange Network Stack Exchange network consists of 179 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careersAlgebra Graph y= (x2)^24 y = (x − 2)2 − 4 y = ( x 2) 2 4 Find the properties of the given parabola Tap for more steps Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = 1 a = 1 h = 2 h = 2 k = − 4 k = 4Algebra Factor x^22xyy^24 x2 − 2xy y2 − 4 x 2 2 x y y 2 4 Factor using the perfect square rule Tap for more steps Check that the middle term is two times the product of the numbers being squared in the first term and third term 2 x
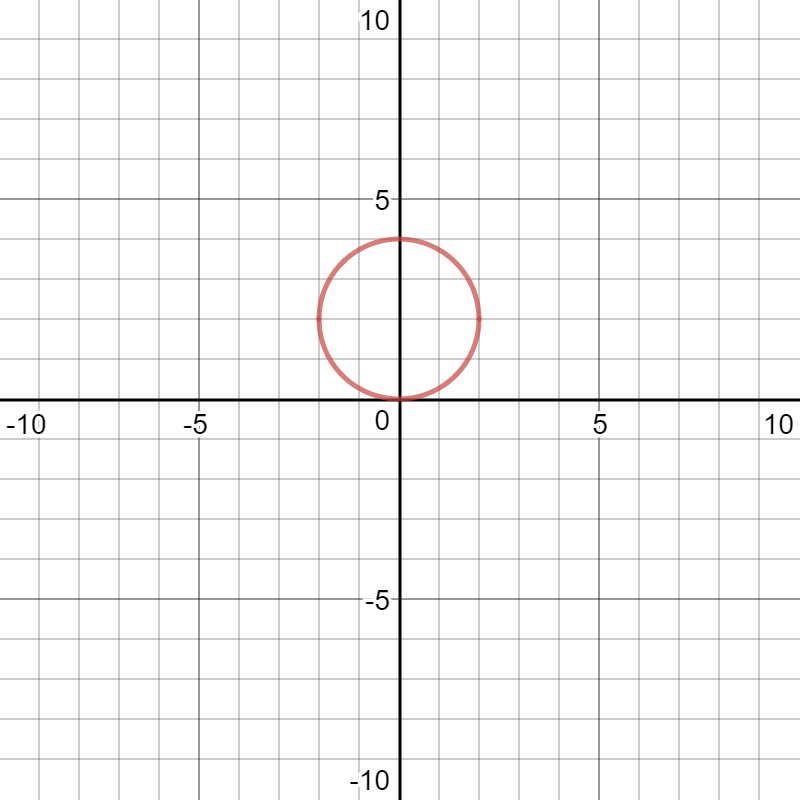
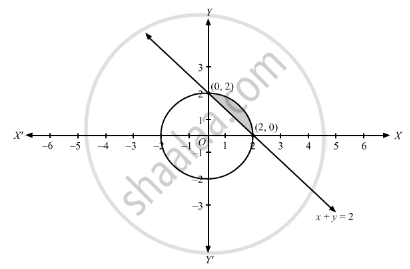
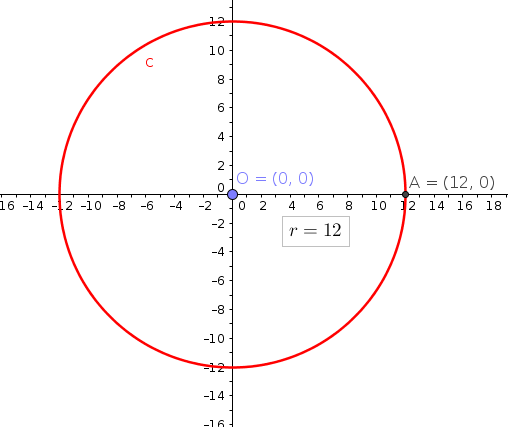
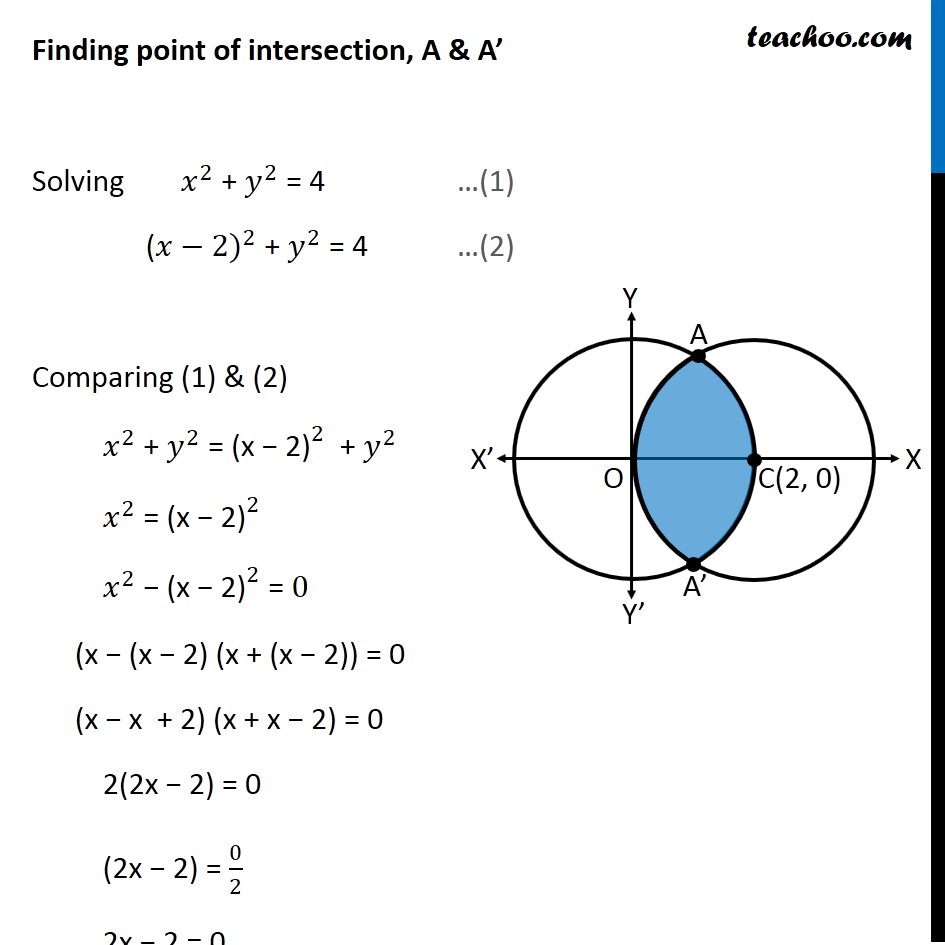
Obviously x 2 y 2 = 4 is a circle having centre at (0, 0) and radius 2 Since ( 0 , 0 ) satisfy x 2 y ≤ 4 Therefore region R 1 is the region lying interior of circle x 2 y 2 = 4 For region R//googl/JQ8NysConverting the Rectangular Equation x^2 y^2 = 4 into Polar FormExperts are tested by
X^2+y^2/4=1のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 | 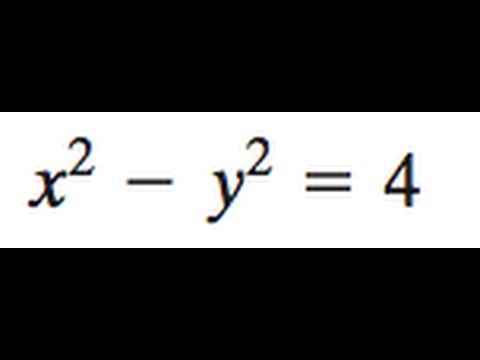 | |
 |  |  |
「X^2+y^2/4=1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「X^2+y^2/4=1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「X^2+y^2/4=1」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 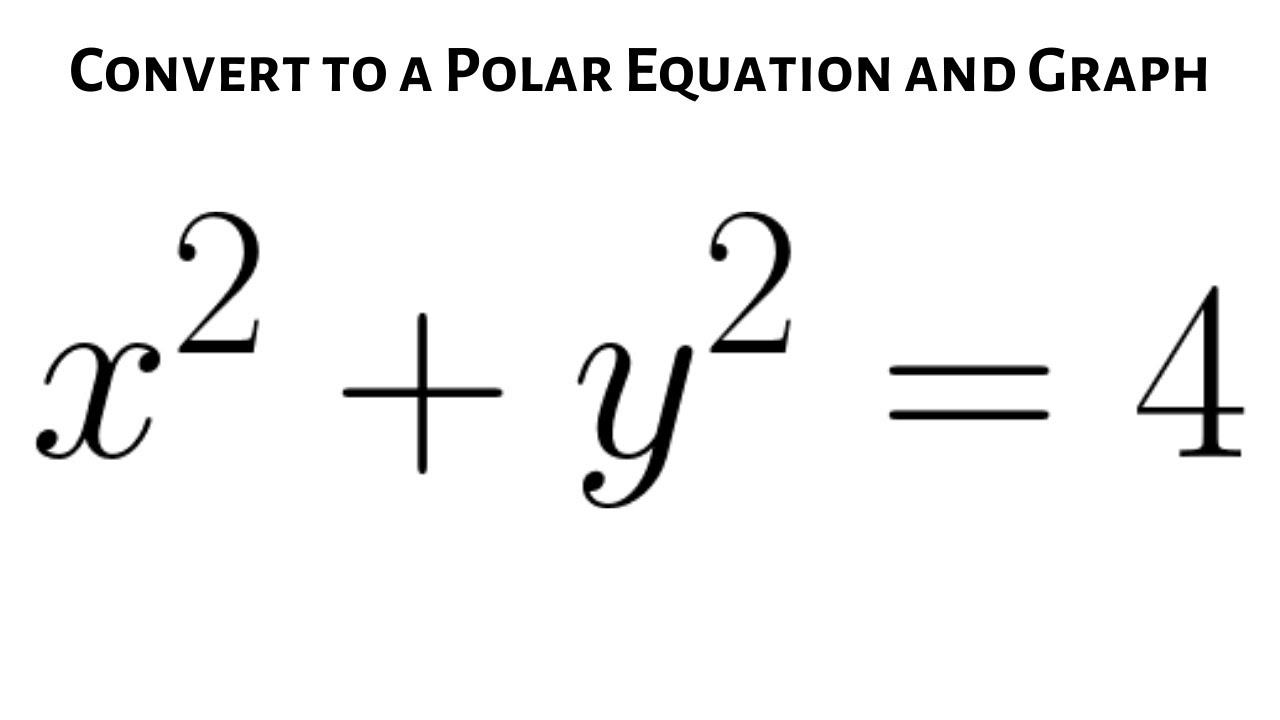 | |
 |  |  |
 | ||
「X^2+y^2/4=1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「X^2+y^2/4=1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「X^2+y^2/4=1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | 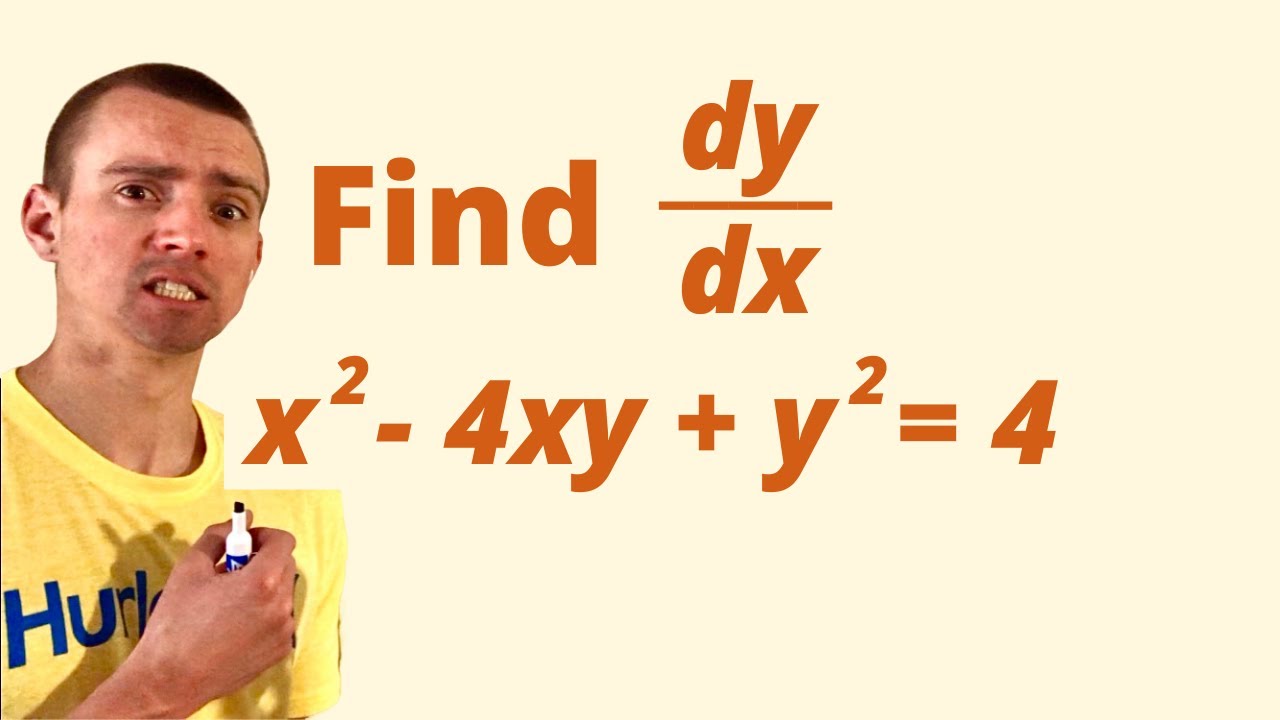 |  |
「X^2+y^2/4=1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「X^2+y^2/4=1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「X^2+y^2/4=1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
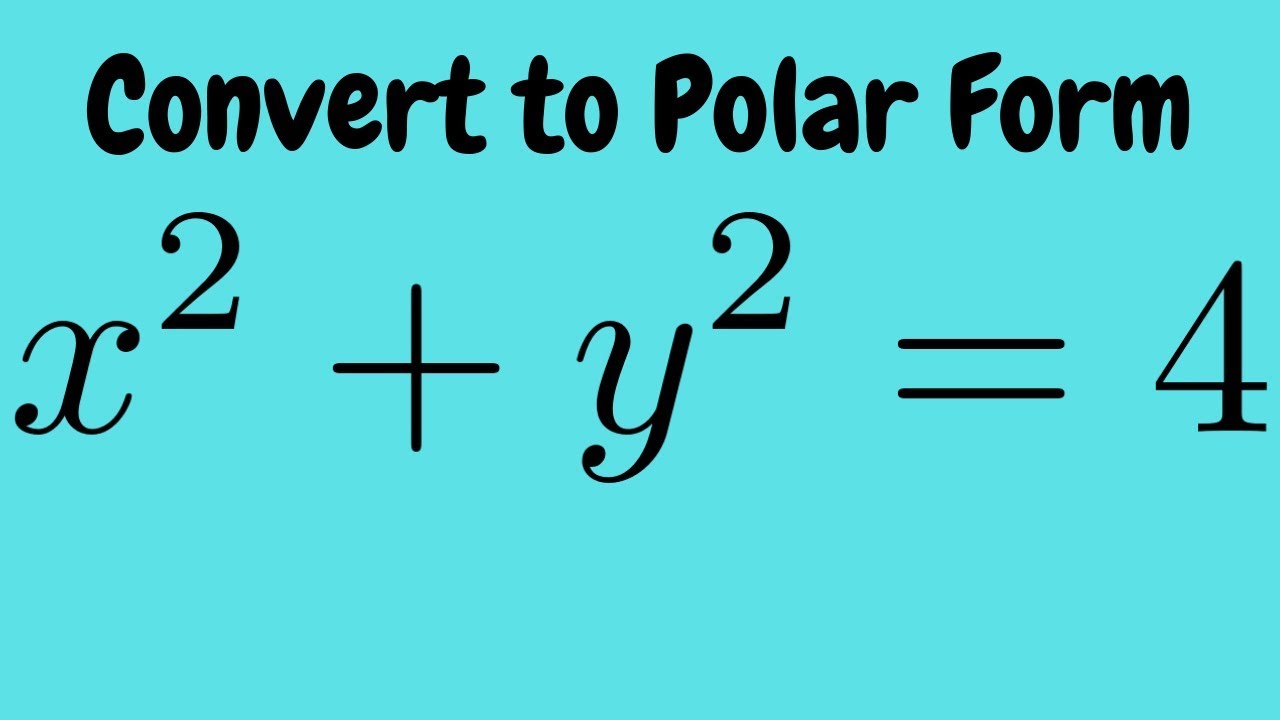 |  |  |
「X^2+y^2/4=1」の画像ギャラリー、詳細は各画像をクリックしてください。
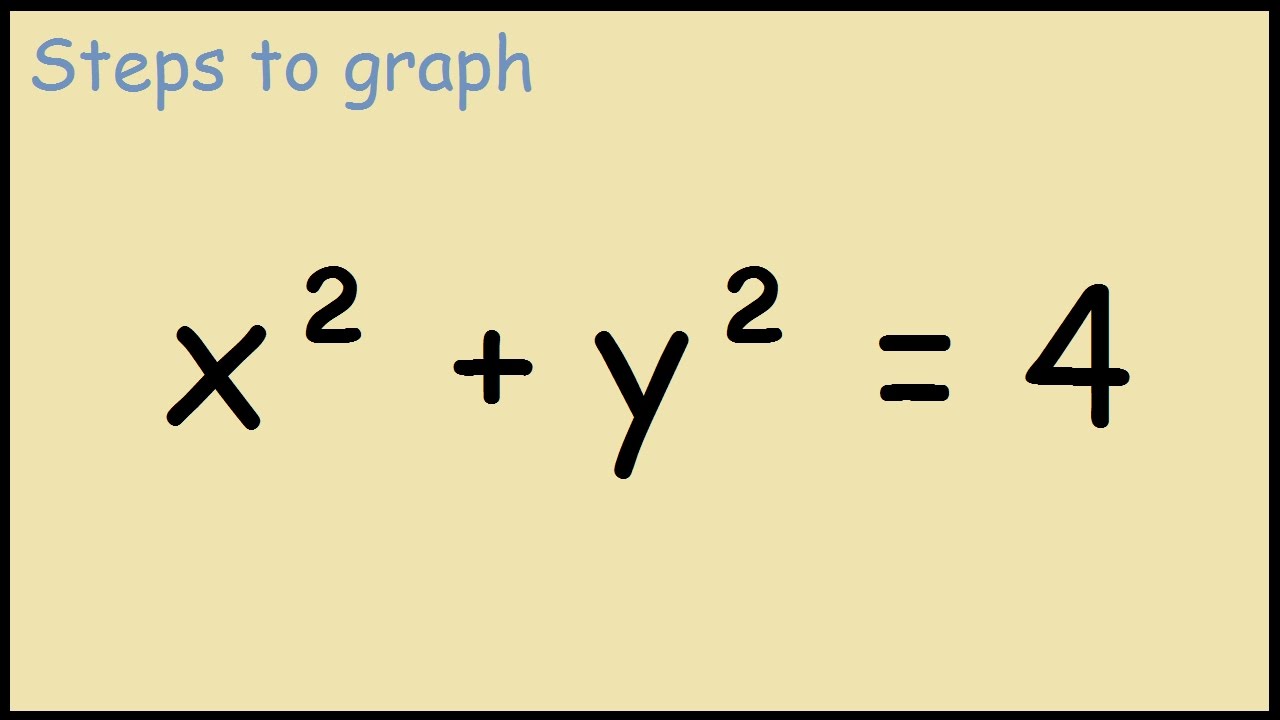 |  | |
 |  |  |
 |  |  |
「X^2+y^2/4=1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
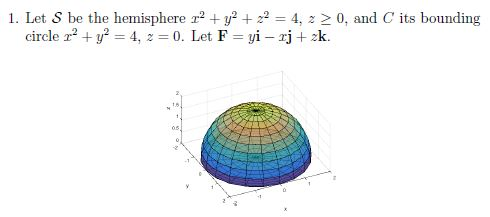
the other equated pairs of terms give us similar relations One solution then is to use x = y , x = z , and y = z in turn to obtain from the constraint equations x x z = 4 ⇒ x 2 x 2 ( 4 − 2 x) 2 = 6 x 2 − 16 x 16 = 6 3 x 2 − 8 x 5 = 0 ⇒ x = 4 ± 1 3 = 1 , 5 3 , as already described in the comments for the posted question One may recognize an ellipsoid, a particular quadric surface If one chooses a cartesian coordinate system, such that the origin is the center of the ellipsoid, and the coordinate axes are axes of the ellipsoid, the implicit equation of the ellipsoid has the standard form x 2 a 2 y 2 b 2 z 2 c 2 = 1 The line segments from the origin to
Incoming Term: x^2+y^2=4, x^2+y^2=4 graph, x^2+y^2/4=1, x^2+y^2=49, x^2+y^2=49 center and radius, x^2-y^2=4 in polar form, x^2+y^2-4=0, x^2+y^2=4 domain and range, x^2+y^2=4 a function, x^2+y^2=4xy,



